上次那篇搞完之后，第二天我尝试了一下算极坐标那个角度的方法，花了很大的功夫尝试了几次，发现特别容易写错，几次写的代码算出来都是错的。我用的那个复数的库，虽然提供了获取长度和获取角度的方法，但是拿到的结果却不是我想要的能直接用于 Ae^ix 形式的。因为反三角函数的值域并不是从0到2π，所以我后来根据实部和虚部的正负关系，配合诱导公式，自己写了实现来求那个角度。思考之后，究其原因，是这东西有二义性。因为我一直假定 A > 0 、也就是极坐标上距离关系那个变量一定是正的，那么 x 也就是固定的了。举个简单的例子，对于 -1 这个数，可以理解为是 1 旋转了 180° 得到的；但是，它也可以理解为是 -1 没有旋转。 -i 这个数，可以理解为 1 旋转了 270° ，也可以理解为 -1 旋转了 90°。所以按照这么说，如果没有对 A 或 x 进行限定，那么就会有不止一种的表示方式。如果计算过程中弄串了，那么算出来的结果就很可能错了（之所以说很可能，是因为也有可能正好是对的）。

不知道是不是搜索方式不对，我网上搜的一些资料直接就跟我说用 arctan 反三角函数来求那个旋转角度。但是就我看，显然是不行的。arctan 是直角三角形中两个直角边的比值，但是当这两个边都是负值的时候……也就是，一个复数的实部和虚部都是负的，在坐标轴中落在第三象限，它是没法分辨出和第一象限（复数的实部和虚部都是正的）的区别的。所以我觉得这种“计算方法”并不能满足我的需求。然后后来我发现，都已经写成 Ae^ix 形式了，那么因为有 A=e^lnA 所以它可以变成 e^lnA+ix 这种形式。好了这下太明显了，一个 a+bi 换成极坐标形式，直接对它取对数，就能拿到 lnA+ix 这样的东西，一个实部一个虚部：虚部是角度，实部是对长度取e为底的对数的结果。然后因为 x 为实数的时候 e^x 是不会为负的，所以这也就满足了刚才说的 Ae^ix 中 A>0 的要求。直角坐标系表示方法取个对数能变成极坐标表示，也是非常的神奇。在C++标准库里，头文件 complex 包含了复数的实现，其中甚至有对复数取对数的函数。

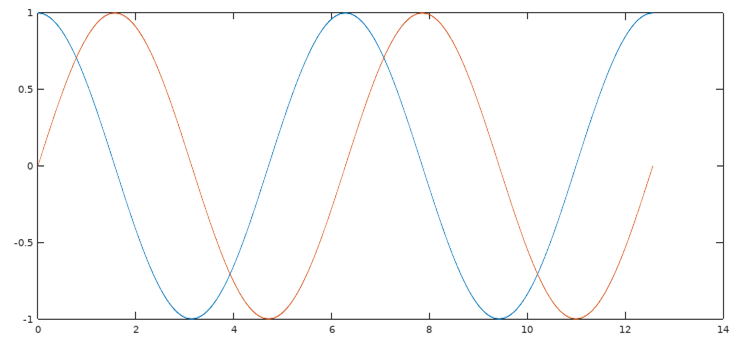
还有另一个就是，我原来一直想不出“复正弦信号”，也就是 f(x)=e^ix=cosx+isinx 的图像到底是什么东西这种事，现在大概知道是什么样子的了。我原来并没有把它放在极坐标看，那么cosx和sinx是两条曲线，我在同一个平面画这两个曲线，最终也就是得到类似这样的效果：

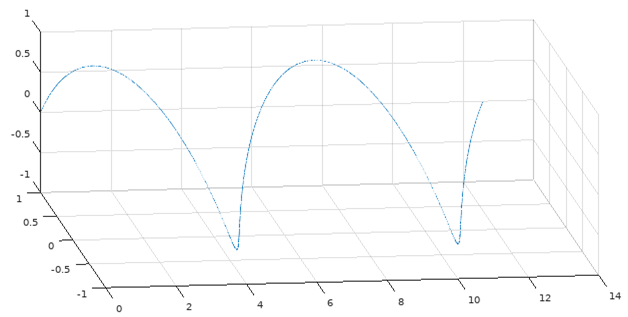
实在是看不出什么东西来，但是实际上，它应该是一个立体的：每个值都是平面上的一个点，然后把这些平面堆叠起来变成一个三维立体的图。它的图应该是这样子的

是像弹簧一样旋转的。所以在实数离散傅里叶变换里，变换后的复数系数里会有一对方向相反（一个顺时针转一个逆时针转）、半径一样松紧程度的弹簧出现。方向相反会使得相加的结果在虚数轴那个方向上相互抵消，最后变回实数。