这几天在看离散傅里叶变换。虽然傅里叶变换那边还没搞定，不过因为数学有好大一部分还给老师了，这甚至都不知道是高中的还是大学的内容，结果这会儿看到复数还得想办法重新去理解复数。当时充其量也只知道个 i²=-1，但是这种程度的理解我觉得显然没办法应付要搞傅里叶变换这种事。今天在学习波形的平移会怎么影响傅里叶变换的结果的时候，好像突然对复数的理解有一点进展了，就赶紧想办法写一写。

我记得我学复数的时候，只知道有个 i²=-1，然后复数是 a+bi （a和b都是实数）形式的东西，在计算的时候如果有遇到两个 i 相乘，就算出 -1，没有的话就把 i 留着。当时也知道两个数轴交叉，横轴是实轴纵轴是虚轴，然而学了还是懵逼，以至于也许我今天理解的东西搞不好就是以前教过还给老师的，无奈只能再来一次。

今天是无意间发现像 a+bi 这种形式的复数，可以写成 A·e^ix 这种形式。对于 e^ix 这种东西的运算，有个欧拉公式，是 e^ix=cos x+i·sin x。按照这个公式逆着来，对于 a+bi 只要有 a=A·cos x 和 b=A·sin x，就可以转化成 A·e^ix 形式。对于这两个等式，很容易可以算出cosx和sinx分别 a/A 和 b/A 。这个时候结合横轴是实轴纵轴是虚轴的坐标系的图，把这个 a+bi 所在位置画上去，再把这个数所在位置和原点连接起来，可以看出这个A其实就是这根线段的长度（我记为L），于是能得出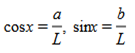，这样很容易就能把x算出来。于是这样就能把 a+bi 转换为 A·e^ix 形式了。

这里其实有个问题，因为 arccos(a/L) 和 arcsin(b/L) 的值域其实是不一样的。在 0~2π 范围内，有两个 x 能让 cosx=a/L，但是并不是这两个 x 都能让 sinx=b/L。所以这里不能只算一个就够了，要分别对这两个等式把 0~2π 范围内两个都算出来，然后取同时满足这两个等式的解。

那么这种形式到底有什么好处，搞得非得把 a+bi 写成什么还能虚数次方的形式呢？其实是这样的，我发现这个 A·e^ix 其实是复数的极坐标式，A是长度，x是和实轴正半轴形成的夹角。

这个图看得就很清楚，i+是虚数正半轴，r+是实数正半轴，c是这个平面上的一个点（一个复数），L是这个复数距离原点的距离，x是拉开这么长距离后，要旋转多少弧度的角。

对于复数的加法和减法，在 a+bi 这种表示方式下更为容易理解：它就和二维向量的加减法是一样的。具体规则是实数部分和实数部分相加，然后虚数部分和虚数部分相加。

但是对于复数的乘法和除法，在极坐标下容易得多。我举个乘法的例子（除法其实是一样的），我有一个 A·e^ix 和一个 B·e^iy 要相乘，运算的时候就变成 A·B·e^i(x+y) ，这样很明显能看出其实是它们的长度相乘，然后它们的旋转角度相加。