红黑树本来来说应该是本科数据结构教学的内容，我当年领到的教科书上也有。但是因为抓得不严，总之最后是不了了之，连有没有教过都忘记了，自己也没有去学。现在过了这么多年，开始找工作了，发现有些公司似乎挺爱问这个的，关于STL的实现我原先一直以为map是靠AVL树实现的，具体是什么书上看来的我也忘记了。只是现在知道了它其实是红黑树也无济于事，因为完全没有去了解过它，一问三不知。现在就突然想起来，想要补一下这方面的知识。

在搜索引擎上面找了一通以后，发现国内的资料基本就那么几个版本，大家抄来抄去，一上来就跟你讲红黑树的性质，为什么这样、这么来的，只字不提。看着实在也很让人郁闷。把这些性质啥的全部硬记下来，然后写一写再体会也不是说就不是办法，但是个人比较讨厌。于是就想上网去找外国人写的教学。Bing搜索的英语版搜red-black tree tutorial这个关键词，然后就找了 http://eternallyconfuzzled.com/tuts/datastructures/jsw_tut_rbtree.aspx 这个来看。在我搜索的时候，这个是第一个结果。点进去看了也是比较容易理解，就决定用这个来学了。最终学习了它的Bottom-up insertion和Top-down deleteion两种操作。

我之前说我不喜欢看一上来就是要记那些性质的教学。上面那个链接里的文章是从B-tree开始的，从这个地方开始能够让人看了很容易知道是怎么回事。

二叉搜索树还是比较容易懂的，一个节点保存一个数据，然后还有左右两个指针，比这个数据小的放在左指针，比这个数据大的放在右指针，然后许多数据通过这种方式关联起来，要找某个数据的时候，就也用同样的方式，从树根开始走，发现当前节点上的数据比要找的数据小，就往右走；发现当前节点的数据比要找的数据大，就往左走。就好像综艺节目里猜数字游戏的时候主持人跟你说“大了”“小了”那样，在最理想状态下每一次比较都能过滤掉数据集里一半的内容，一半一半又一半到了最后剩下一个的时候就是你要找的数据了，或者到了最后没数据了说明你要找的东西在这个集合里没有。

B-Tree不是二叉的，是很多叉的，所以不能单纯用“比它大”“比它小”来说明：这个“它”是谁啊，一个节点里可能不止一个数据的。B-Tree呢一个节点大概是这个样子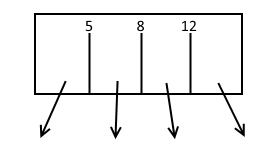

也就是说，本来是一个节点只有一个“分界点”的，现在一个节点可以有n个分界点，由这些分界点可以得到n+1个子树。这里面的5、8、12就是分界点，然后搜索的时候划分出四个范围：比5小、比5大但是比8小、比8大但是比12小、比12大。

红黑树就是从B-Tree变来的，它是从一个节点最多能存3个“分界点”、最多可以有4个子树的B-Tree变来的二叉树。每个B-Tree的节点在红黑树里由一个黑色节点和若干个红色节点组成。也就是说当作B-Tree看的时候，红黑树里的红色节点是算在它父节点（黑）里面的。因为是最多3个“分界点”的B-Tree，所以变成红黑树节点的时候，就有三种情况：只有一个黑色节点、有一个黑色节点和一个红色节点、有一个黑色节点和两个红色节点。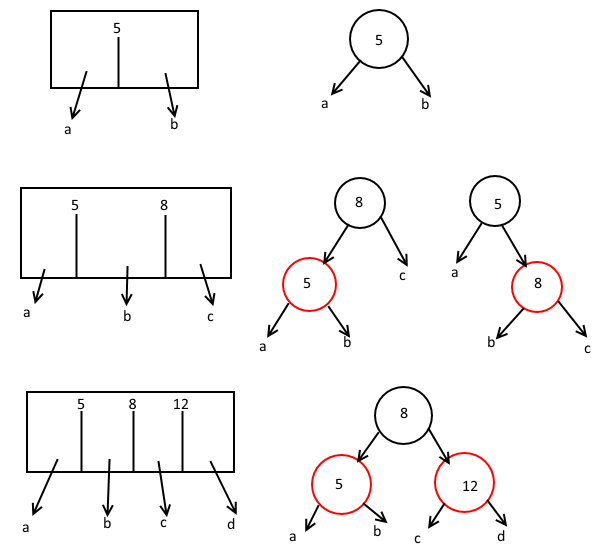

如果要说为什么最后一个不把两个红色节点都画在同一边的话，因为对二叉树来说，深度是越低越好，因为深度越低找数据起来越快，所以如果遇上有两个红色节点都在同一边的情况，就要把它调整成两个红色节点分别在两边的情况。红黑树就是靠不停地调整，在对它进行插入、删除的过程中，保持它代表的B-Tree的每个叶子节点都在同一个深度上。所谓“代表的B-Tree节点”，就是在看红黑树的时候，要把红色节点和它上面的黑色节点看成一个整体……也就是说，从上往下在数深度的时候，遇到黑色算增加一层，遇上红色不算。根节点上面没有节点了，不能把根节点算在“某个黑色节点”的头上，所以根节点一定是黑色的。如果调整过程中根节点变成了红色，可以无条件把它变为黑色：反正已经是根了，深度加一也是两边一起加了，不会影响平衡。

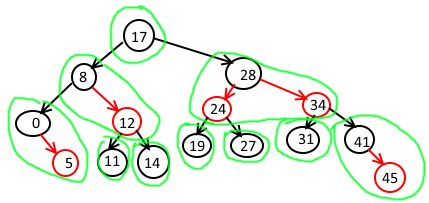
下图是一个我写的程序代码在运行过程中插入了15个随机数之后构建的红黑树：

按照它所代表的B-Tree来看，是这样的

所以它其实是一个三层的B-Tree。

对于这样的二叉树，搜索是不用说了，二叉树一个很重要的功能就是拿来搜索。因为红黑树也只是一个普通的二叉搜索树，所以搜索的时候和其他二叉搜索树没有区别。重点在于插入和删除操作，因为这两个比较麻烦。

先说插入的操作。因为树是深度越低越好，然而黑色算深度而红色不算，于是插入的节点最理想状态就是红色，这样不会增加深度。事情当然没有这么简单，因为红色节点是依附在黑色节点上的，而受到红黑树所表示的B-Tree的每个节点最多只能有三个“分界点”的限制，一个黑色节点上最多只能依附两个红色节点，再多下去就破坏了这种限制，所以当插入的红色节点慢慢增多的时候，调整也就不可避了。

调整的手段是通过旋转二叉树的节点。举个例子，上面那个图，有两个分界点的那个图，它变为红黑树节点的时候有两种表示方法对不对，这两种方法是等价的，从一种表示法变为另一种表示法，也不影响二叉搜索树的性质也不影响红黑树的性质。对于左边的图，把那个8转下来，调整一下颜色，就变成了右边那个图。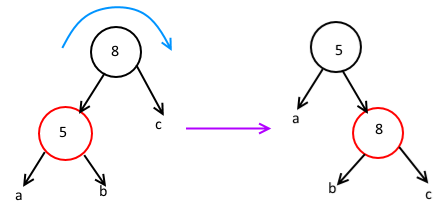

二叉搜索树的节点旋转是二叉搜索树的主要调整方式，通过这种调整，不会破坏二叉搜索树“左边节点小右边节点大”的性质。注意旋转过程中，子节点从一个父节点下移动到另一个父节点下的变化，比如在上图中，b从5那个节点的右边变到了8那个节点的左边，这样的变化规律。

红黑树靠着这种旋转，可以解决两个红色节点都在同一边的问题。例如上面左边那个图，8和5，我要插入一个4，这个4是红色节点，但是插入的地方是在5下面不是在8下面。这个B-Tree节点作为二叉搜索树的一部分来说，效率不够高。红黑树里规定红色节点的子节点不能是红色节点，遇上这样的情况，就通过旋转的方式把这个节点转成符合规定的，像这样：（注：这里的b其实是空的节点，就是不存在的，因为如果b是存在的，那必然是黑色节点，这样就不满足所有叶子节点在B-Tree里深度相同的规定了。c也是同样的道理，因为8下面不能再有更多的红色节点了。为了方便说明b和c最终会到哪里去，这里还是画出来了，因为说到要增加层数的情况的时候，那个4下面就有可能还有节点了）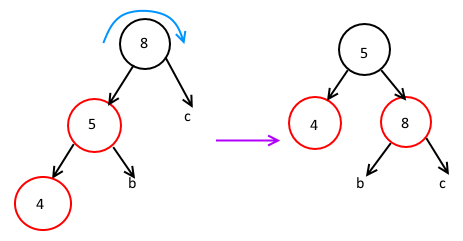

旋转的时候，因为最上面的黑色节点是作为这个“B-Tree节点”表示成红黑树时的“根节点（单个B-Tree节点范围内）”存在的，所以调整之后，和上一层“B-Tree节点”连接的节点还是要刷成黑色的，而其他作为依附在这个黑色节点上的节点，是要刷成红色的，注意其间的颜色变化。两个红色节点的旋转除了这种还有一种情况，比如刚才那个，我这次插入的是6，如果也还是像刚才那样旋转，就会变成（和上面一样，a和c其实是空的）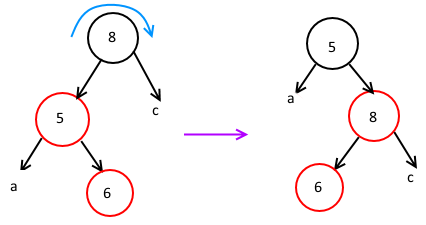

这都转的啥……（扶额）所以也就是说，只有当两个红节点都在同一个方向的时候，才能这么转
所以这种两个红色节点方向不一样的情况，是先转成上面方向相同的那个样子，然后再转一次把它转回来，就像这样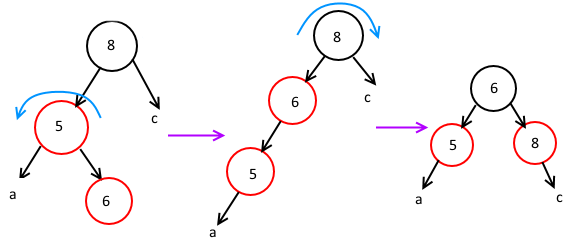

也就是说当两个红节点在不同方向的时候，要这么转两次。注意这两次的方向是相反的。进行这样的双旋操作之后，仍然要注意颜色的变化：和上一层连接的节点要刷成黑色，其他刷成红色。

到这里为止，如果插入的红色的位置不对，已经知道如何调回来了。但是不断这样插入红色节点，想想也不对。因为红色节点在B-Tree里不计算深度的，一个B-Tree不可能一直插入一直插入深度不增加。另外一个黑色节点只能带最多两个红色节点，不能再多下去。所以对于这种已经满了的“B-Tree节点”，红黑树也有自己的处理办法：把它拆分成两个“B-Tree节点”，父节点塞到上一层去。啥叫“塞到上一层”？红色节点不是“依附在别人身上”的吗，那就直接把父节点变成红色节点，这就是“塞到上一层”了。比如上图的6、5、8，如果这个时候我再要插入一个9，就要进行拆分了：5和8是拆出来的新节点，6被塞入上一层。检查是否有两个红节点的操作应该最先进行，因为如果一个B-Tree节点里已经有三个红节点了，那么怎么旋转都没用的。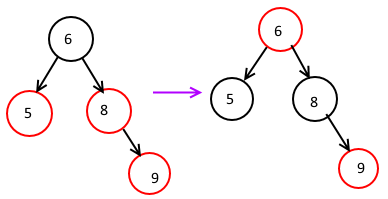

所谓“被塞入上一层”，仔细考虑一下，其实不就是“给上面添加了一个新的节点”吗？于是如果添加以后红色节点过多了，就继续按照这个思路调啊调给调整上去，调整到根的时候，如果根变成红色了，就把它变成黑的：你看这下B-Tree的深度增加了1。红黑树所代表的B-Tree就是这么增加深度的：如果根节点是红的，把它变成黑的。

仔细观察的话，以上三种操作全都是在同一个B-Tree节点内完成，前两个都不会影响节点外的部分，都是节点内部的事；最后一个

在实际操作过程中，规定所有子树，如果是空子树，那么就认为它是一个黑色节点。这样可以在写代码的时候带来一些便利，并且也不影响红黑树的性质。这样就可以开始讨论实现了。

以上谈到的插入操作中，因为插入的总是红色节点，又红色节点不计算深度，所以可能产生的不满足红黑树定义的情况，就只有红色节点过多。归纳一下，插入过程中会遇到的红色节点过多，一共是三种情况。这三种情况都是指“在同一个他们所代表的B-Tree节点里”

1、把两个红色节点插到同一边去了，两个红色节点在同一个方向上
2、把两个红色节点插到同一边去了，两个红色节点的方向不同
3、已经有两个红色节点了，还再往里面插。

最后一种就是把它分成两个“B-Tree节点”。最后一种情况最容易，两个红的换成黑的，再把父节点做成红的。

然后说说前两种情况，因为前两种情况都是旋转，一个转一次一个转两次，那么归纳起来，旋转操作就是：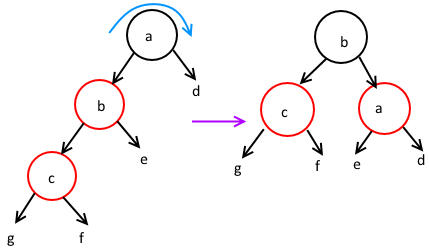

因为旋转之后b节点会作为父节点，而a作为子节点，所以a指向b的指针不应该再指向b；因为在旋转后作为b的子节点，所以b原来的一个子节点e就没有被指了。这样一去一来，正好a原来指向b的指针就指向了e，这样也符合e要比b大、比a小的条件。可以看到，旋转过程中，c的子节点是没有被碰到的。这样说可能比较抽象，那么如果以C++代码表示的话，这种旋转操作其实是和“谁作父节点”相关、可能有两个方向的。若定义树的节点如下

template<class T>
struct Node
{
    T data;
    bool isRed;
    Node<T>* left;
    Node<T>* right;
    Node(const T& val = T()) : data(val), left(0), right(0), isRed(true) {}
    bool IsRed() {
        if (this == 0) return false;
        else return isRed;
    }
};

那么就有

template<class T>
Node<T> *Node<T>::*GetTheOther(Node<T> *Node<T>::*direction)
{
    if (direction == &Node<T>::left)
        return &Node<T>::right;
    else
        return &Node<T>::left;
}

template<class T>
Node<T>* SingleTurn(Node<T> *root, Node<T> *Node<T>::*newRoot)
{
    Node<T> *Node<T>::*theOther = GetTheOther(newRoot);
    Node<T> *tmp = root->*newRoot;
    root->*newRoot = tmp->*theOther;
    tmp->*theOther = root;
    return tmp;
}

template<class T>
Node<T>* DoubleTurn(Node<T> *root, Node<T> *Node<T>::*newRoot)
{
    Node<T> *Node<T>::*theOther = GetTheOther(newRoot);
    root->*newRoot = SingleTurn(root->*newRoot, theOther);
    return SingleTurn(root, newRoot);
}

代码中用到了“指向成员变量的指针”，这样就能比较方便地表示“一个方向”和“另一个方向”而不是写死的“左”或者“右”。如此，同一段代码就能操作两个方向的旋转了……反正它们是对称的。这些代码字面上看是很恶心很难理解，我也是画个图然后按照图写出来的。没图的话光靠脑子想，大概会写错吧……

似乎有点不好理解，说明一下，Node<T> *Node<T>::*newRoot这一个参数中，首先是 Node<T> *，代表参数类型，是指向Node<T>的指针；然后是 Node<T>::*newRoot，代表指向 Node<T> 的一个成员。连起来就是，Node<T>有一个成员类型是Node<T>*，然后这是一个指针指向Node<T>类中的一个类型为Node<T>*的成员。

于是前面提到的插入操作，就可以按照普通的二叉搜索树的插入方法来插入，插入完毕之后原路沿着插入时经过的所有节点，检查有没有前面提到的红色太多或者红色只在一边的情况，有的话把它们调整好。这样插入的代码如下：

template<class T>
Node<T>* Insert(Node<T> *root, const T &val)
{
    if (root == 0)
        return new Node<T>(val);
    if (root->data == val)
        return root;
    
    //get direction
    Node<T> *Node<T>::*direction, *Node<T>::*theOther;
    if (val < root->data) {
        direction = &Node<T>::left;
        theOther = &Node<T>::right;
    } else {
        direction = &Node<T>::right;
        theOther = &Node<T>::left;
    }
    
    root->*direction = Insert(root->*direction, val);
    
    if (root->left->IsRed() && root->right->IsRed()) {
        root->isRed = true;
        root->left->isRed = false;
        root->right->isRed = false;
    } else {
        if ((root->*direction)->IsRed() && (root->*direction->*direction)->IsRed()) {
            root->isRed = true;
            root = SingleTurn(root, direction);
            root->isRed = false;
        } else if ((root->*direction)->IsRed() && (root->*direction->*theOther)->IsRed()) {
            root->isRed = true;
            root = DoubleTurn(root, direction);
            root->isRed = false;
        }
    }
    
    return root;
}

二叉树常用递归的方式进行操作，在递归的操作里面，可以这么看：每次调用自己（函数），调用的时候限定了操作范围：去掉一层节点，把下一层的某个子节点当作是“根”传进函数里，这样函数的操作范围就变成了某个子树；当范围限定到某个叶子节点的空位时，就是找到了应该插入的地方，就可以添加新的节点。插入之后，在不断调整红黑树平衡的过程中，把调整之后的新“根”返回给上一层递归，上一层递归就把这个新的“根”代替作为参数传进函数里的时候的那个“根”（这新的“根”旧的“根”可能会是同一个节点）。

字面上看，就是先用二叉搜索树插入的方法插入，用递归，一层一层找到要插入的位置，然后再递归的回来，一层一层调整，要调整的情况就是前面说的三种情况，调整方法就是单旋转和双旋转，两个红色在同一边相同方向用单旋转，两个红色在同一边但方向不同用双旋转。插入完成后记得要把整棵树的根节点标记为黑色。

这里插入完成之后调整红黑树的部分代码，没有检查子节点是否是空的。因为可以确保的是“这里的root不是空”，并且插入是插入到direction方向，也就是direction那个方向也不会是空。至于再下一层，因为空节点被当作是黑，IsRed这个函数的这种处理方式也不会造成程序出错。所以这里没有判断子节点是不是空的代码。

于是插入操作到这里就结束了。简单体会一下，就是红色节点是“依附”在黑色节点上、和黑色节点一起代表一个“B-Tree节点”的，所以插入红色节点这一种操作，实际上就是在一个这样的B-Tree中，找一个还有空位的节点，把数据插入到这个空位上的操作。当实在没有空位的时候，就会把一个节点拆成两个（就是那个变色操作）来创造空位；插入以后在二叉树层面上效率不够高，就会在节点内进行旋转使得单个节点内平衡。

然后来说删除操作。在插入的时候，是插入一个红色节点，因为成功插入一个红色节点相当于在B-Tree的某个节点的空位里插入了一个数据，这样不影响层数；只在必要的时候才拆节点再插入。这样的话，如果我删除的时候，删掉的是一个红色的节点，那么删掉之前和删掉之后，就能不对红黑树的性质产生影响：因为在B-Tree上来看，删除一个红色节点就相当于在某个B-Tree的节点里删掉一个数据（并且这个B-Tree节点里有不止一个数据）。像这样的操作，是不会影响B-Tree的深度的，同时也不可能造成“在同一个‘B-Tree节点’内同一边有两个红色节点”的情况。但是在删除的时候，又不是总是移除一个红色节点，所以这里的思路是，通过各种调整手段，把要删除的节点调成红色的，然后就可以安心删掉了。这里说的“调整手段”，和插入的时候类似，就是调整后红黑树仍然是红黑树，红黑树的性质不受影响。

在这之前，先说一下普通二叉搜索树的节点删除吧。为什么这么简单的东西要先说一下呢！因为我在学习红黑树之前甚至连普通的二叉搜索树要怎么删除节点都不知道吖（殴

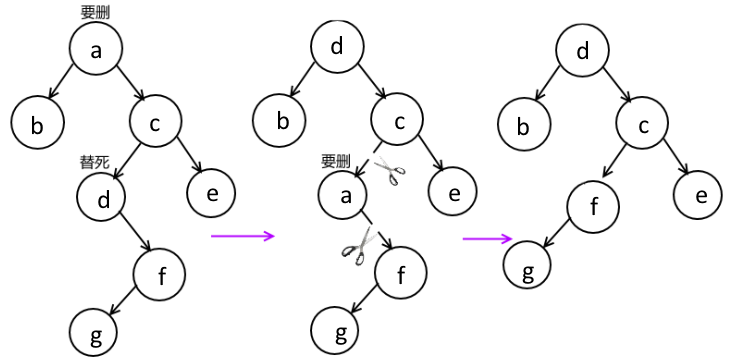
在二叉搜索树里进行插入操作的时候，总是找一个合适的地方插入一个叶子节点：你有在半路上就找个坑蹲着吗（爆）还不都是走到头然后在那个头头上粘个新节点。删除叶子节点我也会，会插入的话脑瓜子想想就解决问题了。但是如果是半中间给你挖个坑，如果这个坑只有一个子节点，左子节点或者右子节点，那么直接把它丢到这个坑里问题就完结了，麻烦就麻烦在它有这么一种情况：同时存在左右两个子节点。对于这种情况，凭借我的脑子仔细（大概有“仔细”？）想了半天，不知道应该怎么办。后来到网上一搜，发现原来很简单，你就到它右子树里找最小的一个节点，把这个节点和你要删除的节点互换，然后把这个节点删掉就好了。所谓右子树里最小的节点，就是先往右走，然后一直一直往左走走到头。既然“到头”了，就说明它没有左节点了，也就是没有比它更小的了，像这样的节点删起来就容易，因为它没有左节点，所以要么已经是叶子要么只有一个右节点，已经是叶子就直接把它咔嚓了，如果有右节点那么用右节点代替它的位置即可。可以这样做的原因，是因为这个二叉树里已经不存在比要删除的节点大但是比要交换的节点小的节点了：第一次往右走就是把范围限定在比要删除的节点大，然后不断往左走到头就是在这个范围内找个最小的，所以下次走到这里，如果要找比这个大的，就往右走，右边不存在比这个节点更小的（以前有个更小的，现在和要删除的节点数据交换后当替死鬼去了……）。到这里，要怎么在二叉搜索树里面删除一个节点，就很明白了：没有或者只有一个子节点的，脑子想想就知道怎么做了；有两个子节点的，就找个只比它大一点点的来当替死鬼……

怕说不清楚，来个图

我尽力了……（扶额

前面已经经历过了插入操作，那么也就废话不多说，来谈谈怎么搞这个删除操作。思路是想办法把“当前的节点”弄成红色的，如果正好当前节点是要删除的并且并不是两个子树都有，那么就可以直接删了，如果是要删除的节点并且有两个子树，那么就往右，继续一路把走过的节点调成红色，直到找到传说中的“替死鬼”，此时“替死鬼”也是红色的了，就可以去替死了……这样说岂不是一路上会有好多红色节点出来？其实不然，因为你在往下走的时候一路在调整，刚刚你调成红色的节点变成了父节点，你把现在的当前节点调成红色的时候父节点（前一轮的“当前节点”）就又变黑色了（因为调整过程中是要保持红黑树的性质的，而红黑树的性质其中一个就是红色节点的子节点不能是红色节点）。

和插入的时候一样，是寻找要删除的元素，走到一个节点的时候，有这么几种情况：
1、要删除的节点就是当前节点
2、要删除的节点比当前节点小
3、要删除的节点比当前节点大
虽然有点废话，不过确实是这三种情况。如果要找的节点比当前节点小，那么就往左走；比当前节点大那么就往右走；如果就是当前节点，看当前节点的情况，如果有两个子树，就往右走（为了去找右边最左的，就是比它大但是在比它大的里面是最小的，找到以后把数据和要删除的节点交换）；如果只有一个子树，恭喜，因为在顺着树行走的过程中，将会使用各种方法保证当前节点是红色的，因为当前节点已经被调成红色了，你可以直接咔嚓了……

没那么容易让你找到的，所以不管是上面说的情况2还是情况3，都要继续往下走。往下走的时候，就会遇上黑色节点了，这个时候就要用“调整”把它调成红色节点。因为之前说过，我们“假设已经把当前节点调成红色”了，也就是说，此时当前节点可能是黑色，但是父节点是刚才调整过的，是红色。借助这个已知条件，就能把当前节点调成红色的。而调整的方法，就是在自己的子节点或者兄弟节点的子节点那边找个红色的来，然后把这个红色的给偷过来（不会是兄弟节点的，因为父节点是红的，兄弟节点再是红的就违反红黑树性质了）。即便这样，也有可能这些都找过了找不到，就比如下图这样。此时就要利用父节点的红色了，把之前插入的时候用的拆B-Tree节点大法反过来用，变成合B-Tree节点大法（其实就是调颜色）：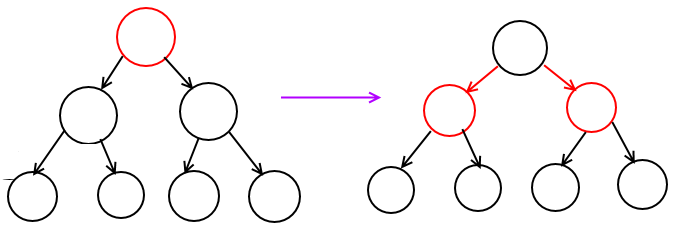

简直机智有没有，从B-Tree层面上看，这个就是先从上面一层抠一个数据出来单独变成一个新的“B-Tree节点”（最上面那个红的变成黑的），然后把下面一层的两个节点给塞进这个“新B-Tree节点”里去（两个黑的变成红的），在这个过程中，变红的两个黑节点的层次在B-Tree中其实和红的变成黑的那个节点在B-Tree中的层次相同，所以这样的调整，B-Tree的深度不变……并且调整时也没有影响红黑树的性质，完璧。搞完以后，“当前节点”就变成红的了，可以继续下一步操作了。

然后再来说说找到了的情况。找到了的话，它有可能在各种地方，比如在当前节点下面，又比如在兄弟节点下面。这两种情况要分开处理。

先来红色节点在当前节点下面的情况。当前节点下面有左右两个子节点，如果你正好要往红色节点那个方向走，万事顺利你可以直接走了，不用调整，因为当前节点已经没有利用价值，虽然你走下一步的时候，父节点（也就是现在的当前节点）不是红色，但是红不红无所谓，因为下一步你将要让它红的已经红了。如果红色节点和你要走的下一步的方向是相背离的，这时还是要通过调整把当前节点调成红色的。方法是在同一个“B-Tree节点”内作旋转，像下图这样，旋转之后，原来的红色节点转到了当前节点所在的位置（这个“B-Tree节点”内新的root），而“当前节点”则转到了它的下面，变成了红色节点←变成了红色节点！重点！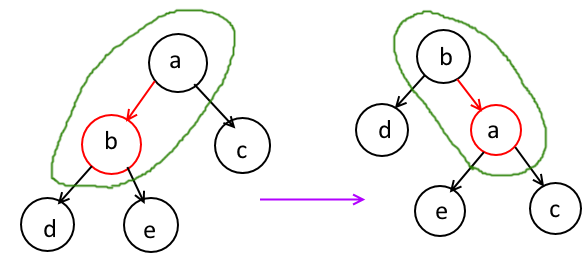

a是“当前节点”，在旋转之后变成了红色。而从B-Tree的角度来看，d、e、c仍然是a和b构成的“B-Tree节点（绿色框内）”的子节点。进行这一步操作的时候，如果代码中有记录父节点和当前节点对于父节点的方向，则要跟着一起调整。没有这样调整的话，程序很有可能就死在这里了。

然后是红色节点在兄弟节点名下的情况。这种情况的旋转牵扯到父节点，并且由于父节点是红色节点，在理解上会比之前的更加困难一些。红色节点在兄弟节点下面也有两种情况：在左边和在右边。为了描述方便，就说和当前节点同向或者反向吧。和当前节点同向指的是，比如当前节点是父节点的左子节点，那么“也在左边”就是同向；如果当前节点是父节点的右子节点，那么“也在右边”就是同向。于是就有了红色节点在兄弟节点下面的位置是和当前节点同向和反向两种情况。

和当前节点反向的情况（注意此时a是父节点，c才是当前节点）：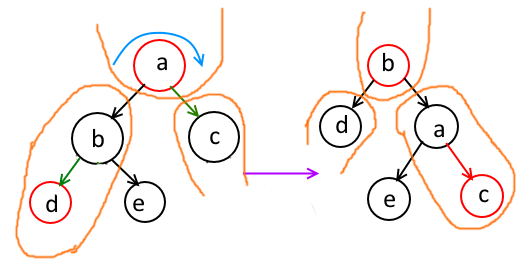

注意其中绿色箭头所代表的“相反”。在这个图中，c代表当前节点，a是当前节点的父节点，b则是它的兄弟节点，图中土黄色圈起来的部分是在B-Tree中属于同一个“B-Tree节点”的部分。这种情况下，父节点是属于当前节点所在的“B-Tree节点”的上一层，而此时兄弟“B-Tree节点”（由b、d组成）有超过一个的数据（两个红黑树节点），这样就可以从中抽取一个数据出来，塞入上一层节点（b被塞入上一层），然后从上一层中把b拿出来，放入当前“B-Tree节点”（就是c），这样“当前B-Tree”节点就有了超过一个的数据（有了两个红黑树节点），并且c不处于这个当前“B-Tree节点”的根部，它就如愿以偿地变成了红色……

以上说了那么多，其实就是一个旋转操作。二叉搜索树的旋转操作是不会破坏二叉搜索树的性质的（就是在某个节点的左边的所有直接或间接的子节点，都要比这个节点小；右边就是都比这个节点大）。但是因为普通的二叉搜索树是没有颜色的概念的，所以到了红黑树上面，就需要遵循它所代表的B-Tree的操作守则，好好地调整颜色。

然后还有最后一种情况：和当前节点同向（注意此时a是父节点，c才是当前节点）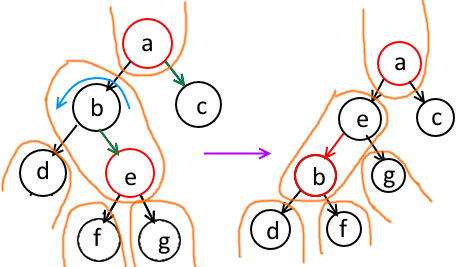

注意其中绿色的箭头，这个箭头就是所谓的“和当前节点同向”。此时如果在“B-Tree的兄弟节点”（就是be组成的节点）内部进行旋转，将原来红色节点那个e转为这个“B-Tree节点”内部的根节点，那么原来的根节点就会跑到另一边去，并且变为红色，……很好，变成上面那种“和当前节点反向”的情况了，于是就用前面那种处理方式进行旋转，当前节点就变红了。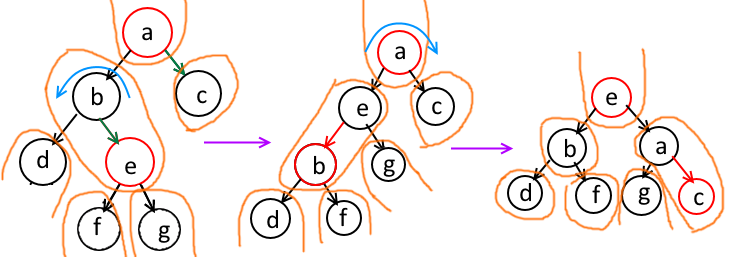

嗯没错，其实还不就是双旋…………

刚才一直在说兄弟节点兄弟节点的，但是有没有要找兄弟节点的时候，兄弟节点不存在呢？其实是不会的。因为找红色节点，是首先从自己这里开始找的，只有自己这里找不到的时候才会开始去考虑兄弟节点。而“找不到”也就意味着，自己的两个子节点都是黑色的了，根据红黑树的性质，往自己这里走有两层黑色节点，那么往兄弟那边走也要有两层兄弟节点才行……如果没有兄弟节点，那么就不存在这“两层”了。

删除操作只有这么几种情况，但是刚才这些删除操作的前提，都是“父节点是红色节点”。但是在操作过程中，最初是从根节点开始的，而根节点一定是黑色。于是就要考虑一下这个黑色该如何处理。对于那种要变色的情况，当前节点为根节点，下面两个子节点都是黑色，可以先把根节点设置为红色，这样如果遇上根节点开始两层都是全黑，就可以把根节点弄黑然后两个叶子弄红了。而对于其他的情况，当前节点是根节点的时候，左右子节点总有一个是红的，那么往下走了一步以后，如果正好走到黑色节点，那么就有“兄弟节点是红色节点”这个条件，按照规则处理就行。有可能会问，如果要删除根节点的话怎么办呢，根节点是黑色啊，你又不调它为红色。嗯，其实没有这个问题的，因为最后移除的总是某个最下面的节点，如果到了要移除根节点，那么这个时候也就是说根节点只有一个子节点了——管它是黑是白，反正根节点没有“上层”了，就算移除黑色节点，也违反红黑树的性质、失去“B-Tree”的平衡。

于是到这里，删除操作也结束了。仔细分析删除操作，会发现和插入操作正好相反：插入操作是先在叶子处插入节点，然后一层层调上来最后调到根部；而删除操作是一层层调下来，最后到了只有一个子节点或者没有子节点的节点变成红色，之后把这个红色干掉。干掉以后，没有其他东西要调整了，所以可以不需要递归，用一个循环，一层层往下。全部搞完以后，和插入一样，把根节点涂成黑色。

这里需要注意的有这么几个方面：
1、变换的过程中，最高可能涉及到父节点的旋转，这样的话，就必须保存父节点的父节点，这样才能在父节点旋转以后，上一层仍然能继续正确指向父节点
2、根节点没有父节点，如果根节点旋转，那么整个树的根就变了。这里可以用一个技巧：创建一个假的“根节点的父节点”，把根节点安在上面，最后搞完了再把根节点从上面卸下来，免去对根节点进行特别处理的麻烦。
3、要保存找到的数据的节点，因为如果这个节点有两个子节点，那么要找“整棵树里比它大但是却又最接近它”的节点来进行数据交换。

为了更方便说明，画个示意图说明最初的时候是什么情况：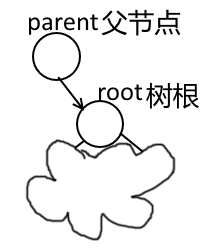

树根在左边或者在右边其实没有影响的……起始的时候，祖父节点（grandparent）是指向NULL，因为在树根是当前节点的时候，是用不到祖父节点的：因为树根没有兄弟节点。所以程序不会出错。如果树根的两个子节点是黑的，那么可以先把树根变红，这样在最初判断的时候就不会因为树根是黑的、要把树根变红而去蹭父节点或者兄弟节点的面子了。那么就可以开始写代码了。

template<class T>
Node<T>* Delete(Node<T> *root, const T &val)
{
    Node<T> fakeParent = Node<T>();
    fakeParent.right = root;
    
    Node<T> *found = 0, *foundParent = 0;
    Node<T> *grandparent = 0, *parent = &fakeParent, *current = root;
    Node<T> *Node<T>::*grand2parent, *Node<T>::*parent2current = &Node<T>::right, *Node<T>::*parent2found, *Node<T>::*current2next, *Node<T>::*current2other;
    
    if (!root->left->IsRed() && !root->right->IsRed())
        root->isRed = true;
    
    while(current != 0) { 
        if (current->data <= val) { //相等的时候往右走，反正之后就一定是一直向左了，毕竟要找的数据小
            current2next = &Node<T>::right;
            current2other = &Node<T>::left;
        } else {
            current2next = &Node<T>::left;
            current2other = &Node<T>::right;
        }
        
        if (!current->IsRed()) {
            if (!(current->*current2next)->IsRed()) {
                if ((current->*current2other)->IsRed()) {
                    //目标节点不是红的但是目标结点的兄弟节点是红的，那么自己转一下，把自己变红
                    current->isRed = true;
                    (current->*current2other)->isRed = false;
                    parent->*parent2current = SingleTurn(current, current2other);
                    parent = parent->*parent2current;
                    parent2current = current2next;
                } else {
                    //到这里，当前节点的两个子节点都是黑的了
                    Node<T> *Node<T>::*parent2sib = GetTheOther(parent2current);
                    Node<T> *sib = parent->*parent2sib;
                    if ((sib->*parent2current)->IsRed()) {
                        //兄弟节点下，方向和当前节点相同的子节点是红的
                        parent->isRed = false;
                        current->isRed = true;
                        grandparent->*grand2parent = DoubleTurn(parent, parent2sib);
                    } else if ((sib->*parent2sib)->IsRed()) {
                        //兄弟节点下，方向和当前节点相反的子节点是红的
                        sib->isRed = true;
                        parent->isRed = false;
                        (sib->*parent2sib)->isRed = false;
                        current->isRed = true;
                        grandparent->*grand2parent = SingleTurn(parent, parent2sib);
                    } else {
                        //兄弟节点下也是两个都黑的
                        parent->isRed = false;
                        sib->isRed = true;
                        current->isRed = true;
                    }
                }
            }
        }

        if (current->data == val) {
            found = current;
            foundParent = parent;
            parent2found = parent2current;
        }
        
        grandparent = parent;
        parent = current;
        current = current->*current2next;

        grand2parent = parent2current;
        parent2current = current2next;
    }
    
    //到这里，current是空的，就是走到头了，parent是最后一个节点
    //如果parent不是found，那么把parent和found交换
    //因为parent只有一个子树或者没有子树了，所以交换后可以直接删掉
    if (found != 0) {
        if (parent != found)
            std::swap(parent->data, found->data);
        
        if (parent->left == 0)
            grandparent->*grand2parent = parent->right;
        else
            grandparent->*grand2parent = parent->left;
        
        delete parent;
    }
    
    fakeParent.right->isRed = false;
    
    return fakeParent.right;
}

这代码看着好长好恶心，确实我也觉得好长，但是由于确实会有那么多钟情况要处理，将就着看吧……

我自己写这个代码的时候，调试过程中被坑了好几次，我在这里就列出几个要注意的地方吧：
1、处理兄弟节点是红色的情况的时候，旋转当前节点之后一定要记得更新记录下来的父节点和当前节点在父节点下的位置。这两个变量没更新的话，下面会死得挺惨的
2、几个旋转过程有点复杂，注意对着图更新节点的颜色。更新颜色很重要，颜色会影响各种调整过程中对红黑树性质的保持，以及会影响如何调整。特别是红色节点在兄弟节点下面的那两个情况，至少我是栽在颜色调错上了：因为里面尽是一些什么“同向”“反向”的
3、当涉及到节点旋转的时候，一定要更新到形如“xxx->xxxx”这样的地方，比如旋转了父节点，就要把旋转后的根节点更新到grandparent->*grand2parent上面去，如果只更新了parent这个变量，那么grandparent到parent的链接就断掉或者说不正确了。这就好像你写了个swap(int, int)的函数不能获得预期效果，要swap(int&, int&)才能获得预期效果是类似的道理。
4、最后交换数据的时候，如果没有足够的自信，请不要去交换节点！交换二叉树的两个节点没有我想象中的那么简单，比如你遇上父节点和它的子节点交换的时候……

里面用的的变量，在图上的话大概是这个意思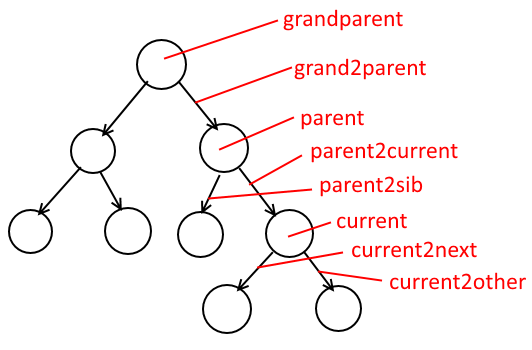

其中一些代表节点，而在连接线上面的代表“方向”，它并不属于某个或某两个特定的节点，它只是代表方向：向左或者向右，任何节点都可以用这样的方向来进行导航。

代码写好之后，想要验证红黑树在整个操作过程中是不是有保持红黑树的性质，也就是说验证代码有没有写错，可以写一个检查函数，在每次插入或删除之后都调用一下这个检查函数来检查红黑树是不是正常，是一个很好的办法。

class RedViolation {};
class BlackViolation {};
class BinaryTreeViolation {};

template<class T>
int CheckTree(Node<T>* root)
{
    if (root == 0)
        return 1;
    if (root->IsRed()) {
        if (root->left->IsRed() || root->right->IsRed())
            throw RedViolation();
    }
    if (root->left != 0 && root->left->data > root->data)
        throw BinaryTreeViolation();
    if (root->right != 0 && root->right->data < root->data)
        throw BinaryTreeViolation();
    
    int lh, rh;
    lh = CheckTree(root->left);
    rh = CheckTree(root->right);

    if (lh != rh)
        throw BlackViolation();

    return root->IsRed() ? lh : lh + 1;
}

这里一共检查三种错误，一种是红色节点的子节点是红色节点，为了保证效率和二叉树层面上的平衡，红色节点只有兄弟节点可以是红色节点，父节点或者子节点都不可以是红色节点；一种是检查是不是符合二叉搜索树的性质，如果旋转操作写错了，那么转出来以后就会出现不符合二叉搜索树性质的情况；最后还检查在B-Tree层面上是不是每个叶子节点都处在同一个高度上，就是说在B-Tree层面上是不是平衡。调整过程中如果红色节点、黑色节点相关的性质被破坏，但是二叉搜索树的性质却没有被破坏（此时可能需要屏蔽一部分检测的代码！因为只要出现任意一种性质被破坏它就会停止检查，还没检查到的地方并不代表就没错！），那么有可能是做的旋转的方向不符合要求，或者是刷颜色的时候刷错了。

最后还要检查红黑树在插入的时候会不会插入重复的节点、删除的时候会不会有些节点莫名消失。方法也挺简单，写一个统计节点数的函数、写一个查找节点的函数（嗯上面只给了插入和删除的代码，没有统计节点和查找节点的。这两个都比较简单，不说应该也没关系吧？XD），插入之前先找这个元素有没有在树里面并统计节点数，如果元素已经存在但是插入之后节点变多了，那么插入操作有问题，查找插入位置的时候找错了或者没有处理元素已经存在的情况吧；删除之前先查找节点是否存在并统计节点数、删除之后看看节点数是否只是少了1，就可以某种程度上判断删除操作有没有问题。从代码上来说应该不会有多删除的问题，因为delete只在一条不带循环的路径上有可能被调用一次。

当然还有更麻烦的错误，就是在操作过程中二叉树已经不是二叉树，变成了有环图、一个节点是好几个其他什么节点的子节点这类，就不怎么好找了。此时可以写一个函数把当前红黑树的情况打印出来，人工检查……虽然很麻烦很累，不过我暂时没想出其他什么省时间省力的做法。

这个是我的完整代码，带测试函数。测试函数会不断循环插入和删除随机数，并且每次操作之后都检查红黑树是否符合要求，这是个死循环，如果程序在运行一段时间后，没有报错崩溃，并且任务管理器中查看这个程序所使用的内存，内存没有不断攀升，那么这个程序应该是没有问题的。

题外话：这本来应该是本科数据结构课程一两次课带过讲完的东西，却学了我快两个星期才学会，简直要满脸血